


For those of you who aren't math geeks, there's a long running battle between educated mathematicians
and inventive idiots like me over dividing an arbitrary angle into 3 equal angles using only a compass
and straight edge.
Sounds as trivial as bisecting an angle, which you probably learned in grammar school, but apparently it
is impossible. Greek mathematicians started trying thousands of years ago and Pierre Wantzel finally
proved it can not be done in 1837.
Yet the battle continues!
A steady stream of trig neophites, unaware of the vast amount of high powered brain hours that have
failed to produce a true trisection, get sucked in by the apparent simplicity and blinding promise
of fame & fortune. I fell into the vortex myself in late 2010 at the Skeptic Society and Marilyn
Vos Savant forums. In spite of embarrassing myself with early simple minded misconceptions, I forged
onward to more complex embarrassing misconceptions. After several months and dozens of failed
attempts, I basicly ran out of ideas and enthusiasm, but it was still simmering at the bottom of my
brain like a ruined reactor core, occasionally belching up a glowing notion that would always turn
out to have some fatal flaw.
Then on Oct 29 2011 Joe Keating posted the topic Trisection of angles-similarly in the
Skeptic's Forum and I was back on the job with a vengence!
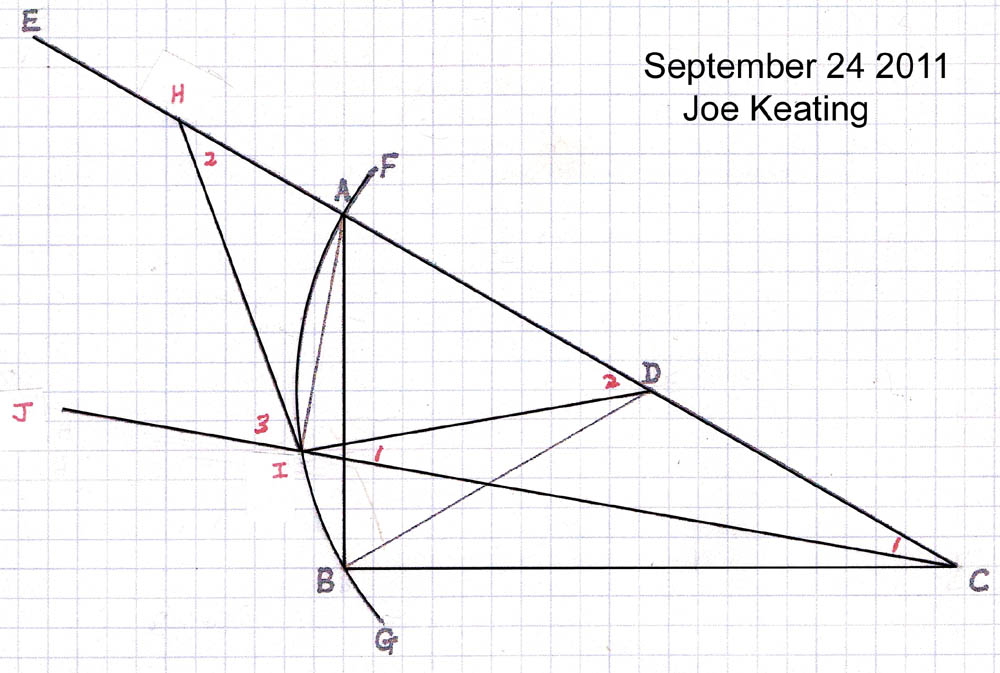
After a few quick tests I realized that Joe was on to something. If not the actual solution, something
so close that I could not see any error. What eventually panned out from several weeks of trials and
assaults on the CR4 engineering forum is that his trisector falls short only in that it is not chopping
a given angle into 3, but rather creating 2 angles simultaniously at an exact 3 to 1 ratio. What the
antagonists still fail to realize is that this is literally a half step away from the real thing.
To help clarify the dynamics, inspire and test ideas, I made 2 copies of a device for Joe and myself.
Click on the pik below to see it in action (and also dispell any claim that its merely tripling an angle).
What the astute will realize is that it becomes a matter of determining that top line. And since the H
point in Joe's diagram is on that line, any other point on the line finishes the job.
For quite a while I was using Photoshop and an actual compass and straight edge with pencil and paper
to test ideas. Very tedius, and, even tho Photoshop can make far finer and precisely located lines and
circles than the physical tools ever could and allows you to zoom in for microscopic views, it was
actually slowing me down. FINALLY I got the C.a.R. program which enabled me to test
and refine trisection ideas properly.
The result is that I have come up with a procedure that gets the angle within billionths of a degree
to start with and has a way to refine this angle by leaps of 10 or even 100 times closer. A feature
inherent in Joe's trisector is that the circle from point D will cross line E C above line B C if
the angle is shallow and below if it is too steep. So instead of having to duplicate the angle you
have come up with 3 times within the original angle in order to see the error, or continually
bisecting your angle for only an infinite series of half as much error, this provides a way to see
the error where it is and 2 ways to quickly draw a much closer angle.
Granted, this is really only like getting into a CaR and driving toward an unreachable destination
instead of walking there, but I'm still experimenting with many other ideas presented by Joe's Trisector.
Here are some Photoshop drawings with the instructions written in Nooalf:
TRiSeKV3INSTR is just the instructions. It will be helpful in making
sense of the CaR files and will download in a few seconds even if you're
on dialup. If you don't read Nooalf yet, go here: Nooalf
TRiSeKV3LO is as low rez as I can make it without it becoming illegible.
TRiSeKV3FLaT is a crisp 1000 dpi picture if you want to see good detail.
It's 8 meg, so go do something else for 5 or 10 minutes if you are on DSL.
Here are the latest versions of TRiSeK V3 in CaR:
The MQVUBL one can be adjusted just by using the move tool (the dot and curved arrow button at the top)
to slide point A along SRKL 1. It should show up as a red X. If not, its the little circle in the
middle of the red circle on the black diagonal line. Hold the left mouse button on it to move it around.
It's virtually impossible to pick a specific angle like this, so I also made USiNDaNGL (assigned angle)
so you can right click on the main AB angle and type in whatever angle in the edit box. I named
everything the same as in the Photoshop drawing on the 'alias' line in the edit box. You will notice
that the oRK V1 location is different from what is shown in the Photoshop drawing.
The CaR software is free and is very ergonomic. I was able to start using it in 5 minutes!
There's way more to it than I've learned how to use so far. My compliments to Rene Grothmann and his
team of programmers. (Or did he make the whole thing all by himself?!)
Mathematicians can still claim that the angle is not being perfectly trisected. But if it is
not possible to measure the deviation, what does that mean? Better computers and more expensive
software can probably find the error and refine the angle many more times than my setup can. I'm
still experimenting here - coming up with refinements and variations on this proceedure and completely
new ideas. Joe also occasionally sends me a new idea to test, and who knows how many young
wippersnapper trigonometry savants are out there who could find an exact method. Because I'm not
amazingly smart and yet have come so close, I suspect that it can be done.
Page originally posted on January 7th 2012. Edited and updated as warranted
Having fun yet? If you want to talk about this, I suggest joining Marilyn's or the Skeptics forum and
jump into the topics already there.
Saturday, Jan 14 2012
It really pays to do the CaR tutorial. Today I discovered the move tool, thus eliminating a bunch of
work building new test angles from scratch. I edited the above stuff from January 7th because the
.zir Car files I had listed don't download and they were outdated versionz of the TRiSek anyway.
Wierdly, TRiSeK V3 works to about 104.4º. Substantially less accurate, but I would have expected
it to completely collapse even slitely above 90º.
I've been working on finding shorter processes and hopefully more accurate. I've come up with 3 or 4
substantially different ones that are reasonably accurate without refinement and I am of course
still hoping for a revelation that leads to a perfect trisection.
This one SIMPL8 has only 8 circles and 8 lines to get within a
thousandth of a degree. It relies on a variation of the refinement process. It gets more accurate as
you approach zero, but is over .2º off at 90. Of course, you could divide angles in half or quarter
or 1/8 etc., run this process and then multiply the rezult the same number of times to get extreem
accuracy. Plus, the refinement process can be used at either or both stages.
A few gliches I've encountered with CaR: 1. Sometimes the angle measure will flip to the other side,
so you see 145 instead of 35, for example. All you have to do is find the first angle point and slide
it back over to the other side of the base point. 2. With a new version I'm working on the software
will flip a circle over when the angle is over 76.5, making the trisek angle not be a trisek angle
anymore. 3. The measure of the angle in the edit box got stuck at 9.something, so now I only get to
see 10 decimal places.
January 24 2012
DaMIT!!!
At about 1:30 this morning I was pretty sure I had it. Every angle I tried was exact. No decimal places,
just 20º, 24º, etc., even 30º for a 90, which is where TRiSeK V3 is least accurate!
But now, around 4 pm, the computer has changed its mind. It now shows errors after 13 decimal places.
Here's how it went:
For the last week I've been grooving to the sites and sounds of my YouTube favez on shuffle and working
on what I call the 'crooked line perspective' in which the AZ line is considered as 2 or more segments
in order to show direction and amount of error and hopefully lead to a way to precisely correct this
crookedness. Then a few days ago Joe sent me this:
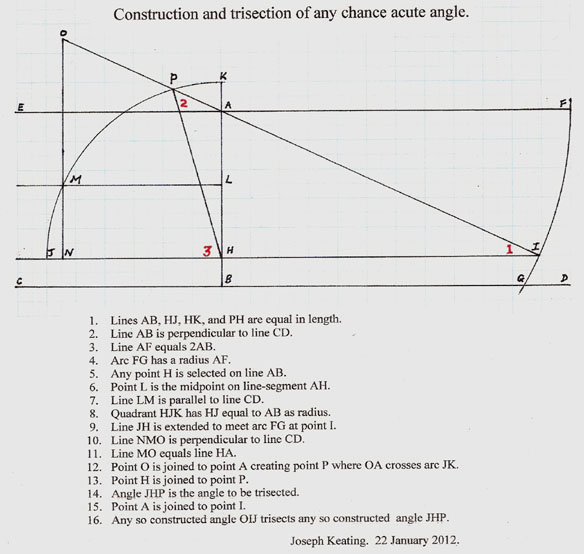
Completely different, yet looking as 'almost there' as the first one! I did a quick CaR construction to
verify it: Joe's New Trisek. Move the red X up and down.
Amongst my first thoughts was that it could possibly be combined with the TRiSeK V3 to produce 100%
unquestionable trisections. The key feature is the new connection to the top line by the OM vertical
line. I was on my way to doing something more complicated wen I decided to try a line from this new
O point to the CD oRKZ- intersection. Like majik it showed perfect numbers.
So, after watching Magnum Force, delivering a job and getting some sleep, here I am again looking at a
reeeeeellly close almost insted of perfection. Some how during the intervening hours, 15º
degenerated into 14.999999999999918º. 30º is now 30.00000000001º. In the daylite, my
Nobel prize in the booming field of applied trigonometric twangularificationology is really a tarnished
video arcade token. Perhaps the ghost of Wantzell was granted a few moments of influence to kibosh this
threat to his accomplishment by the Adjustment Bureau, tweeking my computer's brain just enuff to
thwart me again. OR, quite the opposite and far more likely, the little gremlin in my computer was
fooling me with 'perfect' angles to get a few laffs.
Need to get Kolchak on the case....Waitaminit.
Just had another idea. And wuznt I working on a more complex arrangement before I tried that shortcut?
January 31 2012
None of the more complicated ideas worked. Tried a very convoluted contraption that was perfect at 54º,
but useless at any other angle. Spent the last 4 days making the Photoshop drawing for V4. I also
tested it in a new way that goes far beyond what the software shows in numbers.
Gotta get some sleeeep. I've been in this chair so long I'm starting to waddle like Roger from American Dad.
-------------------------------------------------
I'm back.
First, download one of these so you can get an idea of what I'm yammering about:
V4 INSTR instructions only - no diagram.
TRiSeKV4 LO Good enuff if you aren't planning on framing it.
TRiSeKV4 PRINT pre-rotated for your convenience.
TRiSeKV4 HR 500 dpi Photoshop version.
This is actually less complicated than the V3, but I broke the steps down to their real individual
steps instead of combining similar concurrent ones. You will notice there are several lines and arcs
less than in V3. Simplification AND improved performance is always a good sign that you're getting
close to a finished product!
Some of the errors indicated on the 24th were bogus - likely a rezult of having a bunch of erzatz
features crowding up the construction during development. Errors shown now above 81º and below
about 27º are likely real. But within the range of about 33º to 72º, the best test I
have devised shows the construction to be perfect. (see the drawing) The trouble is that it relies on
the accuracy of an angle drawn with the fixed angle feature of the software, which does all its
calculations at only 16 decimal places maximum. The test is millions or billions of times more
accurate than that, so the way the program calculates and draws things becomes the limiting factor.
The only reliable confirmation I have is that it's not likely to be a coincidence that the angles
match up perfectly. But what about the errors it does show below 27 and above 84? Is it real or the
software miscalculating the V4 process? The test has produced inconsistent rezults, sometimes
showing completely different circle sizes for the same angle. And something wierd happens around
76.5º - the RS line transitions from below the fixed test angle, which originates at point A, to
above it. So somewhere around 76.5 it should be right on the line, yet the software will not do it.
In one attempt this morning, it completely freaked out and erased everything! Luckily, restarting it
brought back the last saved version.
As I have been informed, all CAD software runs at the same limits of precision, so I can't just buy
something to take this to the next level. The goofball fraze 'you can't get there from here' actually
makes sense in this case. I am ruluctantly forced to learn trigonometry now. Learning stuff!
What a pain in the brain!
Feb 1 2012
Joe sent me a boomarang. There was an incident.
I have a headache, but I'm still working on refinements. What I'm looking for now is an alternative
or variation for the CJ JK lines; something that stays at a consistent relation to the true trisek
line on SRKL4
Feb 4 2012
Picked up some math books at from the library. Marilyn Vos Savant's book about Wile's proof of Fermat's
last theorem. Also has some related stuff about cranks like me trying to do impossible stuff. Also got
an actual math book to maybe learn something.
I succeeded in improving the CJJK lines. Now it reads perfect over the whole range. Beyond actually,
since it goes to 103 with 10 decimal places correct. At 104º it has a 5 at the end instead of 7.
I named it V4.1, like the software convention I've alwayz hated. Makes sense since I'll probably come
up with a better refinement in a week and then some new revelation will lead to a trisector worthy
of a V5 designation.
I'm not going to do the Photoshop thing for this. Instead, I'll email the CaR file to anybody who's
interested. Breifly, the diference is the blue CJ JK lines are based on little circles now which keep
the L point closer to where it needs to be.
Another thing I came up with this week is pretty obvious - put a test circle at a million kilometers!
I tried a billion, but the software fails somewhere before that. It shows things there, but points
jump around and things dont line up. A million is good enuff to show errors anyway, still assuming
the fixed angles are precise.
I was testing ideas at 9º, 45º, 60º and 90º. V4.1 is 187 quadrillionthsº
under for a 9º (2.999,999,999,999,813). At 45 the test radius is .1586mm at point A and .0877mm
at 1 million km. At 60º its .382mm and .189mm. At 90º its .5813mm and .5059mm. An interesting
detail is that the line is below the A point till about 76.6º, then shifts above it. Same with V4,
and I tried to zero in on an angle where its right on, but couldn't. That would be the angle at which
the blue AN1 line would be a perfect trisection.
Later, same day.
Seems I have already exceeded the computer and software's accuracy. I ran the V4.1 on my new Toshiba
NB505 netbook and it produces different numbers. The 9 degree came up with 3.000 000 000 000 068º.
Very significant that it's on the other side of 3º. Then I made a new one on the old Dell with
1,000,000 radius circles instead of only 1,000 and at 9º it says 3.000 000 000 000 186º.
Want more accuracy? WeL, YU KANT GIT XAR FRUM HYAR!
-----------------------------------------------------------------
On Feb 1, xouper from the Skeptic's Forum challenged Joe and I to construct triangle CID starting with
only HIJ (see Joe's first trisek sketch). His claim is that Joe's thing is really only a version of a
marked ruler trisection and that we would find it impossible.
Here you go, xoup: Xouper's Challenge
February 6 2012
Originally posted in Marilyn Vos Savant's forum about 20 minutes ago in response to naysayers:
I'm reading Ms. Vos Savant's book about Wile's proof of Fermat's last theorem.
Very revealing insight into the world of math. Not the absolute prestine clarity of logic us laymen
assume. Instead, everything is based on uncertain axioms, other proofs that aren't 100% accepted,
and mind bogglingly complex labyrinths of thought that defy any sort of visualization.
If the simple, fundamental idea of parallelism is in doubt, why would anybody think that this
trisection impossibilty proof is unquestionable?
Think of it this way: If little old me can get to quadrillionths of a degree in a matter of months with
a 16 step construction, how far could a few thousand cooperating real brainiacs get in 10 years with
no limit on how many steps their construction could have?
Or: I'm just churning thru ideas here one at a time. An existing program or a specially designed one
could do the same thing a trillion times faster.
All the other trisection attempts I've seen are very simple constructions. The basic assumtion on the
entire subject is apparently that there should be some simple trick of geometry that produces a perfect
trisection.
Why should it be simple? Why should it even make sense? Especially, why should it make sense to our
limited intelligence? It only has to work.
Why would someone who is well educated in math expect a 'proof' that it works when much more fundamental
concepts have no proof and others have proofs that fill books and aren't universally accepted?
My contention today is that a bunch of perfect trisection methods can be created, but 'proving' they are
perfect will be impossible for humans.
Feb 8 2012
Turned the computer off and was going to leave it for a week, but I couldn't get the 'filter stage'
idea out of my head.
Since my computer can't refine the final line and the L point can't be improved, what if some sort of
pre-refinement could work? A filter stage to purify the brew before bottling. I seemed to get a good
result once, and then it was coming up with seriously lousy numbers, like only 10,000ths of a degree.
I'd become confused with the steps and the computer seemed to be bogging down, so I thought a
week's vacation would help.
I couldnt pay attention to anything, so gave up last night and fired up the Dell. Ran the Registry
Booster and started work on the filter stage.
It seems to work. 'Work' meaning that it seems to be more accurate than V4.1. Not sure, because of the
limited measurment accuracy of the computer and CaR, but it was consistently showing above perfect
measuring from one side of the angle and below from the other. (14.999999999995 and 15.000000000001 for
example). At 45, The gap between the final line and the software generated fixed test angle was the
same at 1 million km as at point A (.00311), and at 90, everything lined up - the 30 degree fixed
angle, the 'pre line' from the filter stage and the final trisecting line. Gap = zero at A and the 3
lines were so close together at a million km that the computer couldnt line up any new points with
anything there.
So I made a fresh construction. It doesn't measure the same as the prototype, but it's the correct steps.
I made the html with more functions this time. Click on the left and right trisecting angles to see the
different decimal places. You can replay the whole construction, zoom with the mouse wheel, measure
other angles, add new stuff etc. Notice the invisible circle.
I would like to see how it does in other programs - SolidWorks, Pro-E, Vellum, other geometry programs -
anything thats made to do precision drafting work. I can email the CaR file or step by step
instructions if this example isn't enuff. JO 753 at ZoL inc.

Feb 11 2012
Started reading Dr. Underwood Dudley's The Trisectors last
nite. His stated purpose is to dissuade people from trying.
"Well, it didn't work." begins the addendum to the introduction
for the second edition. A good laff in the intro usually indicates
a memorable read
Underwood, my friend, you have only been stoking the fire.
Exchanged some emails with Mark Stark - a man who really knows
his trig and created a trisector that is superior to mine back around
2000, 2002. I'm sure he'd like me to make it clear that he wouldn't
call it a 'trisector' but a 'trisection approximation', no matter
how precise it is.
And it is fantasticly precise!
Mark Stark's Trisek. Right click on the black angle
line to change it.
MS MQVUBL. Left click on the red X. Click on the
forward/reverse tool to bring up the construction replay. (I only did the second reiteration on
this one, so the numbers may not be exactly 3 to 1)
Good thing I didn't stumble across this before! I would probably not have bothered to do any of this.
Too bad I didn't stumble across this before! No telling what I would have accomplished with all the
time I've spent on this. There's an idea for you, Underwood!
You will see immediatly that it's way simpler than any version of my trisek. It's also good all the way
up to 180º and accurate to 13 and sometimes 14 decimals for everything above about 12º.
It gets down to only 8 when dividing a 1º. Also, CaR seems to like it. It measures
consistently no matter where you put the points on the lines.
The consistency gave me an idea. Its always under by about 15 quadrillionthsº, so what if you run
the procedure from both legs, double one of them, then go way far out and divide a chord line between
the 2? The error would then only be the difference between a precise line trisection and the arc that
it should be, which at that distance over that narrow of an arc would be like 1/16th of a gorram
planck length, gorramit! (planck length = 1.616 199(97) x 10-35; a unit so small,
the late great wild eyed detail maniac, Theodore Wildi, didn't bother to include it in his book,
Units & Conversion Charts!)
It took me a few hours of trying, but I did it. I had to put a perpendicular line 10 million kilometers
out to see a gap wide enuff to work with, and the computer couldn't line the points up correctly, at
least what it showed on the screen. It kept freezing up & I'd have to Ctrl/Alt/Del to shut the program
down. Same thing several times trying to measure it. Finally I got it to at least try, but it came up
with numbers that don't add up. For a 90 degree, it came up with 30.000 000 000 000 018º
from the final line to one leg and 59.999 999 999 999 986º to the other.
Adds up to 4 quadrillionthsº over 90º.
Mark said that not even 1000 decimals is good enuff, but I think some serious mathematicians must
be thinking 'but maybe if....' about Wantzell's proof.
Febuary 15 2012
I'm about half way thru the 'budget' (catalog) section of The Trisectors. Not the best writing
you will ever read, but entertaining if you're a mathematician or have trisectionitis. The truly
amazing thing is how wide the variety of attempts are. An idea anybody should get from that is 'what
if I combine this one that is always 3% over with that one that's always 3% under and bisect the 2
approximate angles?'
I'm getting an inkling of why Professor Dudley doesn't do an analysis on the more complicated
trisections, even if they seem to promise greater accuracy. A relatively simple one tranzlates
into a long equation, so what would my TRiSeK V3 look like?
I'm starting to feel like I'm done, or maybe 'cured' is a better way to say it.
I did a little test earlier. I drew 2 specified angle lines on either side of The final line in V5 half
a millimeter apart - the width of the led in a fine line mechanical pencil. A look at the 3 lines 5
million kilometers out and the final line is still well within this width; noticably off center, but
how would CaR draw it on another computer? Or how would it turn out with a different program?
To put it in perspective for the non math geeks who have somehow made it this far down the page,
.5mm is the width of 5 human hairs and 5 million kilometers is about 12 times farther than the moon.
On top of that, the TRiSeK V5, and many of the trisections in Dudley's book, could be refined with
the same steps I did with Mark Stark's trisector. Even if a new rule were imposed that limits the
action to the local construction, we still have at least Mark's & my refinement steps to take the
accuracy past the end of the universe.
So I no longer feel the urge to jump on the computer whenever I get a foggy notion about lines and
circles intersecting. Not every little geometry factoid I learn gets thrown into the TRiSeK blender.
The molten corium has spread out, seperated, disapated and diluted into relatively inactive blobs.
I'm still quite interested and will likely update this page occasionally, but unlike many of the poor
slobs in Underwood's book, I can move on to other crazy obsessions!
Sunday, December 24, 2018
Found this page all mangled up, so reconstructed and updated it. Haven't heard from Joe in years.
The CaR files don't seem to work with my Windows 7 computer. They still work on XP, so I'm guessing
that it's something with security concerns and modern browsers wont run the Java. If you're really
interested, I can send the files one way or another.

_|